Self-Improving Embodied Foundation Models
Appearing at NeurIPS 2025: Two-stage post-training for Embodied Foundation Models (EFMs)
- Stage 1) Supervised Fine-Tuning (behavioral cloning + steps-to-go prediction)
- Stage 2) Self-Improvement via online RL with self-predicted rewards and success detection
Foundation models trained on web-scale data have revolutionized robotics, but their application to low-level control remains largely limited to behavioral cloning. Drawing inspiration from the success of the reinforcement learning stage in fine-tuning large language models, we propose a two-stage post-training approach for robotics. The first stage, Supervised Fine-Tuning (SFT), fine-tunes pretrained foundation models using both: a) behavioral cloning, and b) steps-to-go prediction objectives. In the second stage, Self-Improvement, steps-to-go prediction enables the extraction of a well-shaped reward function and a robust success detector, enabling a fleet of robots to autonomously practice downstream tasks with minimal human supervision. Through extensive experiments on real-world and simulated robot embodiments, our novel post-training recipe unveils significant results on Embodied Foundation Models. First, we demonstrate that the combination of SFT and Self-Improvement is significantly more sample-efficient than scaling imitation data collection for supervised learning, and that it leads to policies with significantly higher success rates. Further ablations highlight that the combination of web-scale pretraining and Self-Improvement is the key to this sample-efficiency. Next, we demonstrate that our proposed combination uniquely unlocks a capability that current methods cannot achieve: autonomously practicing and acquiring novel skills that generalize far beyond the behaviors observed in the imitation learning datasets used during training. These findings highlight the transformative potential of combining pretrained foundation models with online Self-Improvement to enable autonomous skill acquisition in robotics.
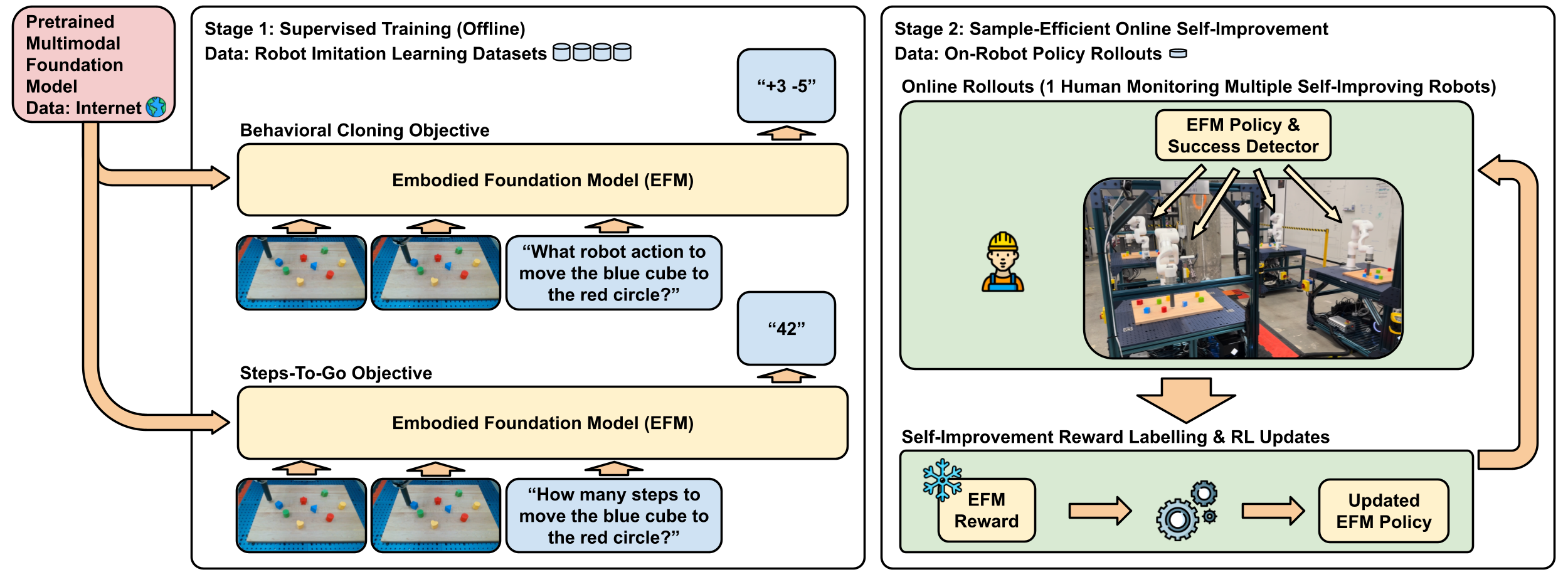
Method — Two-stage post-training
Stage 1 — Supervised Fine-Tuning (SFT)
Fine-tune an Embodied Foundation Model (EFM) initialized from a web-scale pretrained multimodal foundation model with two objectives:
Behavioral Cloning (BC) loss. \[\mathcal{L}_{\mathrm{BC}}(\mathrm{EFM})\;=\; -\,\mathbb{E}_{(o_t,a_t,g_{t'})\sim\mathcal{D}}\,\Big[\,\log p^{\mathrm{EFM}}_{\mathrm{action}}(a_t\mid o_t, g_{t'})\,\Big]\]
Steps-to-go loss. \[\mathcal{L}_{\mathrm{steps\text{-}to\text{-}go}}(\mathrm{EFM})\;=\; -\,\mathbb{E}_{(o_t,a_t,g_{t'})\sim\mathcal{D}}\,\Big[\,\log p^{\mathrm{EFM}}_{\mathrm{steps\text{-}to\text{-}go}}(\,t' - t\mid o_t, g_{t'}\,)\,\Big]\]
Stage 2 — Self-Improvement (Online RL)
Self-predicted rewards and success detector enable robots to autonomously practice downstream tasks and improve online with minimal supervision.
\[ d(o,g)\;:=\;\mathbb{E}_{\;p^{\mathrm{EFM}}_{\mathrm{steps\text{-}to\text{-}go}}(\,\text{steps-to-go}\mid o,g\,)}\big[\,\text{steps-to-go}\,\big] \]
Reward function. \[ r(o_t, a_t, o_{t+1}, g) = d(o_t, g) - d(o_{t+1}, g) \]
Success detector. \[ \mathrm{success}(o, g) = \mathbb{1}[\, d(o, g) \le s \,] \]
This eliminates manual reward engineering and, combined with web-scale pretraining, enables behavioral generalization beyond imitation data.
Key Results
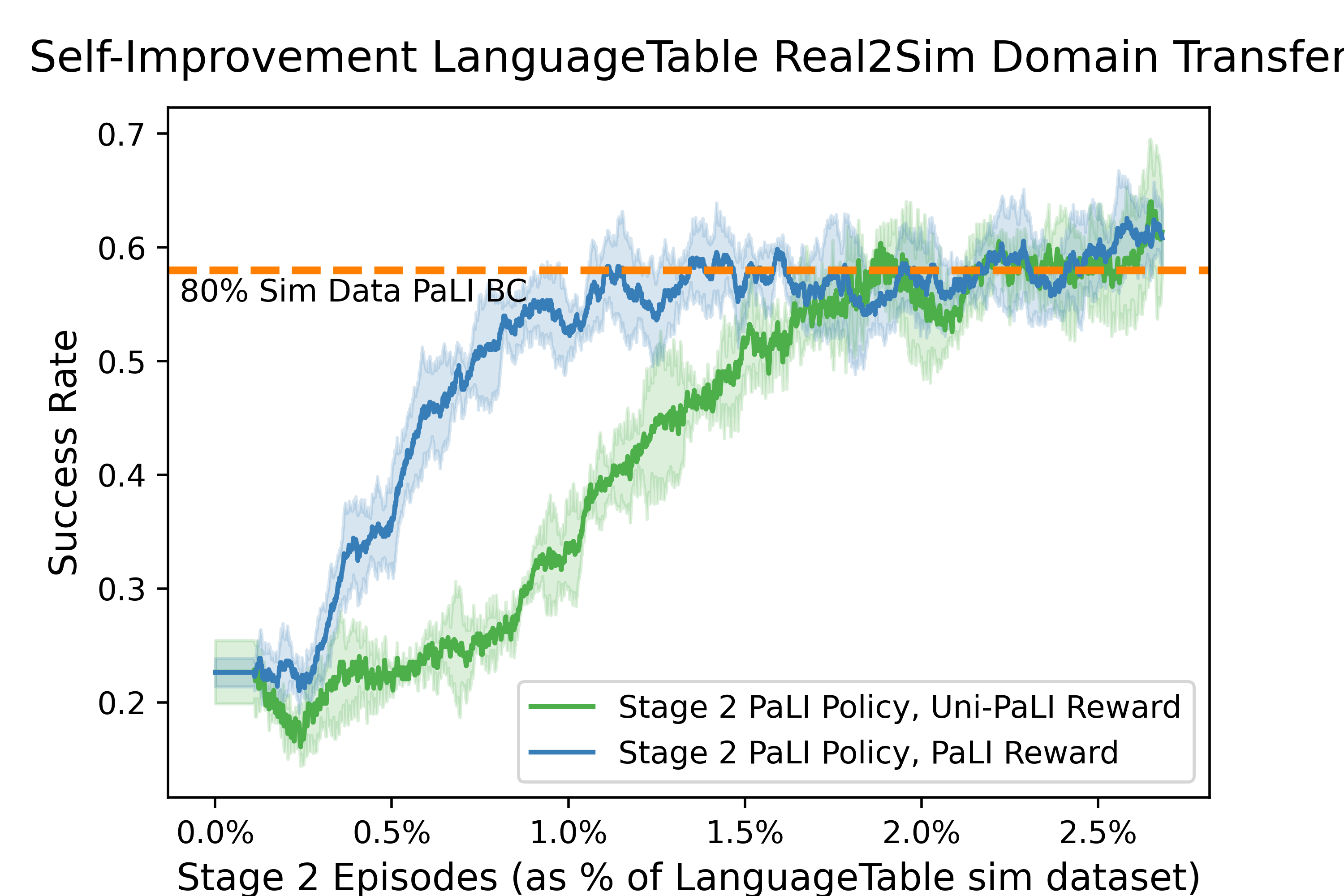
KR1 Self-Improvement significantly improves policy performance beyond Supervised Fine-Tuning (SFT), and the combination of SFT + Self-Improvement is much more sample-efficient than supervised learning alone.
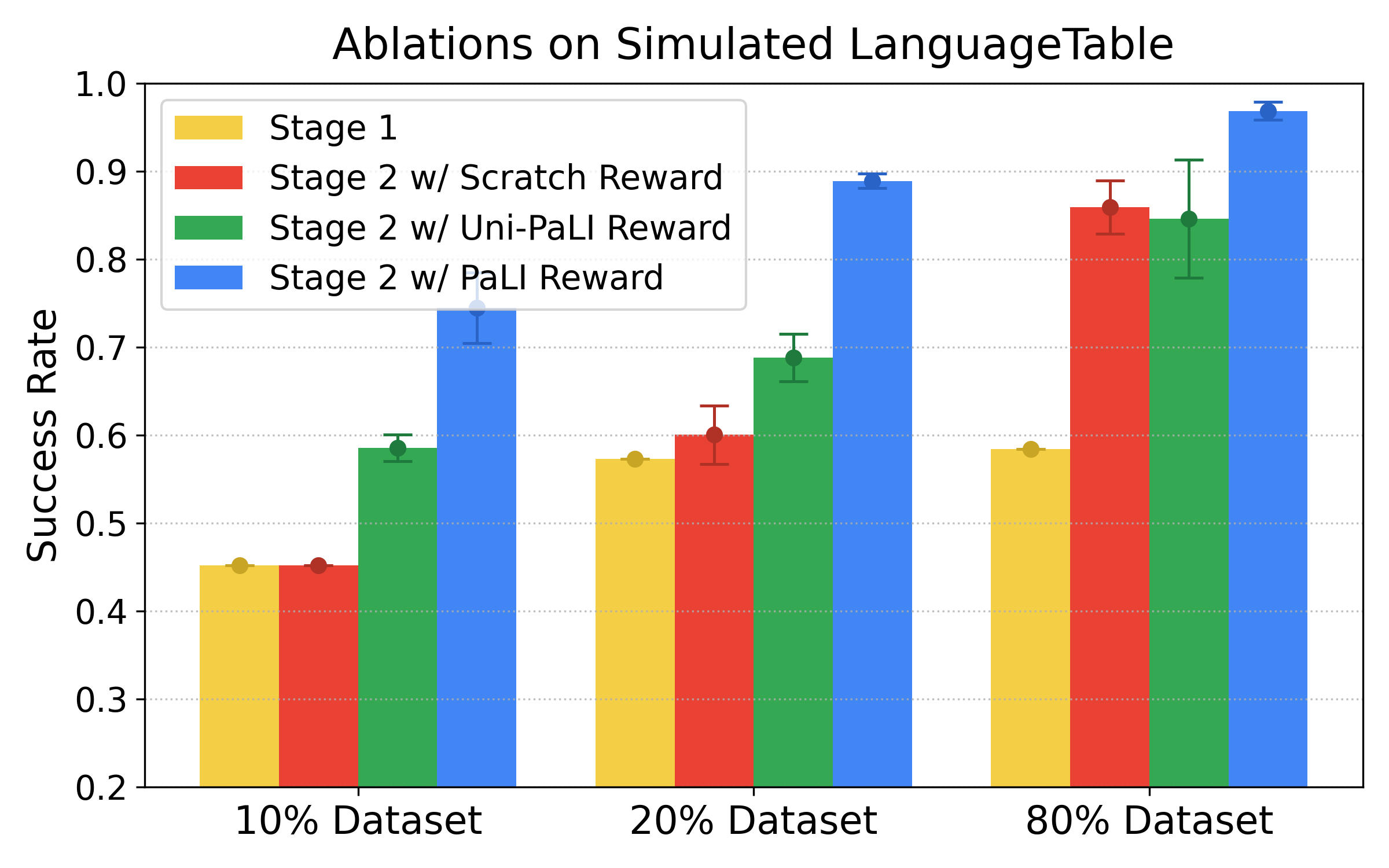
In the Simulated LanguageTable domain, starting from a behavioral cloning policy with a success rate of 45%, we observe:
KR2 Self-Improvement is robust and effective for real-world robot learning.
In the Real-World LanguageTable domain, starting from a behavioral cloning policy with a success rate of 63%, we observe:
KR3 Online Self-Improvement + web-scale pretraining enables policies to rapidly acquire new skills that generalize far beyond imitation datasets.
Generalization across simulation and real-world with Self-Improvement.

Acquiring novel skills beyond the imitation datasets.

We start from a policy and reward model that has only seen the LanguageTable dataset, and never seen a banana nor LanguageTable without the blocks. After 8 hours of Self-Improvement, the model rapidly aquires the novel challenging skill of effectively moving the banana around the table.
KR4 Multimodal pretraining is a key enabler of sample-efficiency and stronger Self-Improved policies.
We ablate alternative reward-model variants. Our results demonstrate the significant value of web-scale multimodal pretraining, in particular on smaller dataset sizes.
- PaLI / PaLI-X: pretrained multimodal foundation models (arXiv).
- Uni-PaLI: vision and language components trained unimodally, without joint training.
- Scratch: no pretraining, same architecture.
Visual Intuition
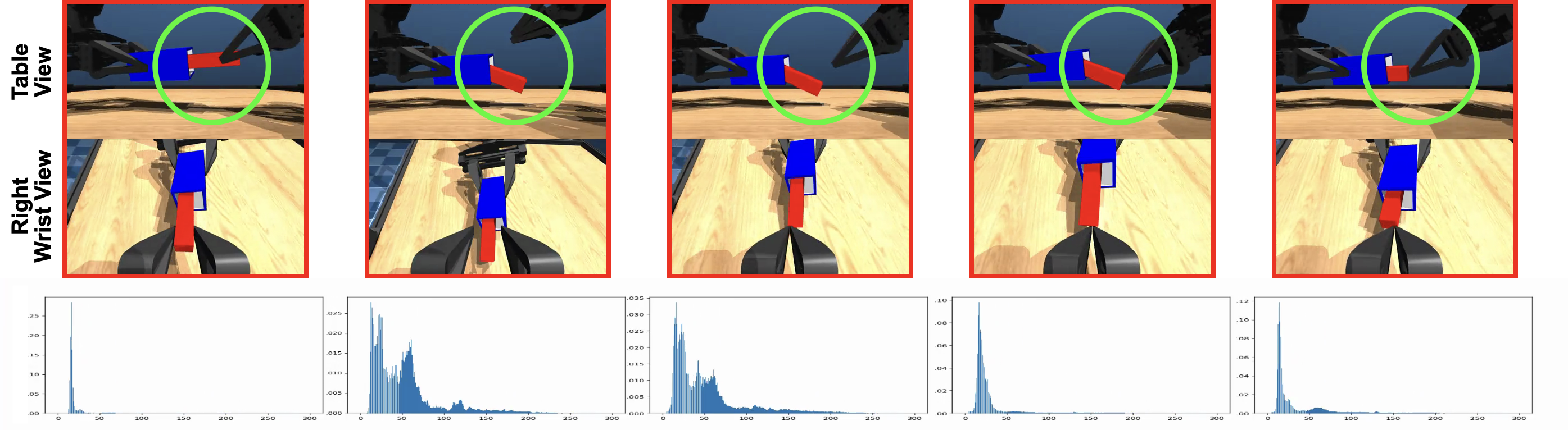


Mathematical Intuition
We use the expectation of the model's steps-to-go predictions:
\[ d(o, g) := \mathbb{E}_{\;p_{\text{steps-to-go}}(\,\text{steps-to-go}\mid o, g\,)}\big[\,\text{steps-to-go}\,\big] \]
To define the reward function as the improvement in steps-to-go:
\[ r(o_t, a_t, o_{t+1}, g) = d(o_t, g) - d(o_{t+1}, g) \]
This also lets us define success detection via thresholding steps-to-go predictions:
\[ \mathrm{success}(o, g) = \mathbb{1}\,[\, d(o, g) \le s \,] \]
Letting \( \mu \) be the policy corresponding to the imitation dataset (e.g., human dataset), we can define the value function of \( \mu \) as follows:
\[ V^{\mu}(o_t, g) = \mathbb{E}_{\mu}\Big[ \sum_{i=t}^{T} -\, \mathbb{1}\big[\, o_i\ \text{satisfies}\ g \,\big] \Big] = \mathbb{E}_{\mu}\big[ -\, \text{steps-to-go} \big] =: -\, d(o_t, g) \]
This enables us to decompose our proposed reward function:
\[ r(o_t, a_t, o_{t+1}, g) = V^{\mu}(o_{t+1}, g) - V^{\mu}(o_t, g) = \underbrace{(1 - \gamma)\, V^{\mu}(o_{t+1}, g)}_{\text{core reward}} \;+\; \underbrace{\left[ \gamma\, V^{\mu}(o_{t+1}, g) - V^{\mu}(o_t, g) \right]}_{\text{reward shaping}} \]
Self-Improvement leads to policies that achieve intended goals more efficiently than the dataset policy \( \mu \), while being implicitly regularized to stay close to regions of the state space where \( \mu \) is proficient.
Simplifying the Monte Carlo returns we observe a built-in baseline subtraction:
\[ R_t = \sum_{i=t}^{T} \gamma^{\, i-t}\; r(o_i, a_i, o_{i+1}, g) \;=\; \Big[\, (1-\gamma)\, \sum_{i=t}^{T} \gamma^{\, i-t}\; V^{\mu}(o_{i+1}, g) \,\Big] \; - \; \underbrace{V^{\mu}(o_t, g)}_{\text{baseline}} \]
The built-in baseline subtraction leads to lower variance estimates, enabling use to use REINFORCE for policy improvement.
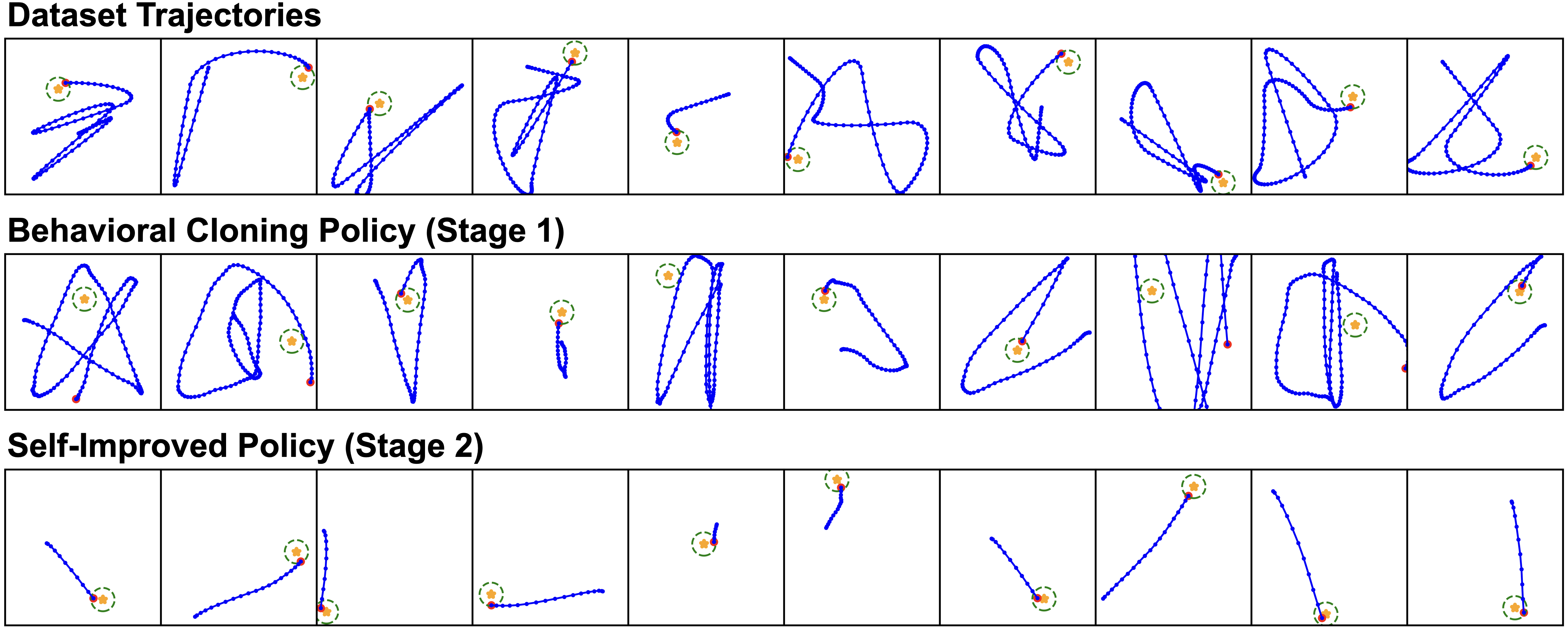
PointMass Domain
We provide a self-contained Colab notebook that demonstrates Self-Improvement on a pointmass navigation domain. Each episode starts from a random position and aims for a randomly sampled goal. We intentionally construct a sub-optimal imitation dataset by using a PD-controller that visits five intermediate waypoints before heading to the goal. We then fine-tune an MLP policy and a steps-to-go prediction model with our two-stage recipe. As expected, Stage 1 BC mimics the dataset’s sub-optimalities, while Stage 2 Self-Improvement (without ground-truth rewards) quickly drives policies close to optimal. The figure below shows sample trajectories from the dataset, BC (Stage 1), and Self-Improved (Stage 2). The videos below show the Stage 1 and Stage 2 policies.
Resources
@inproceedings{self_improving_efms_2025,
title={Self-Improving Embodied Foundation Models},
author={Seyed Ghasemipour, Seyed Kamyar and Wahid, Ayzaan and Tompson, Jonathan and Sanketi, Pannag and Mordatch, Igor},
booktitle={NeurIPS},
year={2025},
note={Appearing in NeurIPS 2025},
url={https://arxiv.org/abs/2509.15155}
}
Authors
Seyed Kamyar Seyed Ghasemipour (Generalist), Ayzaan Wahid, Jonathan Tompson, Pannag Sanketi, Igor Mordatch (Google DeepMind)
Contact: kamyar@generalistai.com
Equal supervision noted in the paper.
Common questions
What is steps-to-go? A model prediction of remaining steps to reach a goal. Its decrease across time forms a dense progress signal.
How are rewards computed? By differences in steps-to-go: r = d(o, g) − d(o′, g).
How is success detected? When d(o, g) ≤ s, providing a principled termination signal.
Why not just use more imitation data? Shaped signals and online practice deliver larger gains with less data collection.
Which embodiments? LanguageTable and Aloha, in simulation and real-world.
Limitations? Mis-calibrated d and latency constraints; addressed via thresholds, filtering, and local inference (Infra v2).
 View on GitHub
View on GitHub